SPE Namespace Reference

Namespace containing all functions and data classes for this solver. More...

Data Structures
struct	Mat_4terms
	structure for 4 mats to have u_term, v_term, w_term, P_term Mat More...
class	SPE
	Class to contain various variables for SPE solution. More...

Functions
PetscInt	Ax_b (const PetscScalar *const *Ain, Vec &x, const PetscScalar bin[], const PetscInt &n)
	Solves \(x\) in \(Ax=b\) linalg problem using PETSc in parallel Useful for solving small systems of equations, such as finite difference coefficients for given stencils. More...
PetscInt	Ax_b (const Mat &A, Vec &x, const Vec &b, const PetscInt &n)
	Solves \(x\) in \(Ax=b\) linalg problem using PETSc in parallel. More...
PetscInt	Ax_kBx (const Mat &A, const Mat &B, PetscScalar &kr, PetscScalar &ki, Vec &xr, Vec &xi, PetscScalar target=0.54213+0.082968 *PETSC_i, PetscInt nev=1, EPSWhich which=EPS_TARGET_MAGNITUDE)
	Solves \(x\) in \(Ax=kBx\) eigenvalue problem using SLEPc in parallel. More...
int	base_flow (SPE &data)
	set plane channel or blasius boundary layer flow velocity variables \(U, U_x, U_y,\) and etc Note: type_base_flow has an integer flag that corresponds with the following flow types More...
int	_bblf (const PetscScalar input[3], PetscScalar output[3])
	Blasius boundary layer function to integrate. Similarity Blasius ODE broken into three coupled equations \[ \begin{aligned} f'' &= \int -ff'' d\eta\\ f' &= \int f'' d\eta\\ f &= \int f' d\eta\\ \end{aligned} \] . More...
int	base_flow_dim (SPE &data)
	Use this after base_flow(data) call to set the ny matrices to size dim. So U is set into U_dim. More...
int	calc_Closure (PetscScalar &I, SPE &data, Vec &q, Vec &qp1)
	calculate the closure equation \( \int_{\Omega} \hat{\textbf{q}}^\dagger \hat{\textbf{q}}_x d\Omega \) and output the result More...
int	calc_L2 (PetscReal &error, Vec &x1, Vec &x2, PetscInt n, NormType type=NORM_2)
	calculate the \( L_2 \) norm of the difference between \(x_1\) and \(x_2\) vectors and return More...
int	calc_L2 (PetscReal &error, Mat &x1, Mat &x2, PetscInt n, NormType type=NORM_2)
	calculate the \( L_2 \) norm of the difference between \(x_1\) and \(x_2\) matrix diagonals and return More...
int	calc_LST (SPE &data, PetscScalar target_alpha, PetscScalar &alpha, Vec &qp1_OSS, Vec &qp1)
	calculate the Local Stability Theory (LST) Orr-Sommerfeld Squire equations in primitive variables at this x-location and store the alpha and qp1 of the target spatial values. More...
int	Create_grid (SPE &data, PetscScalar deltay=0.)
	create y and z grid and stretch in y direction using stretching if deltay is nonzero More...
unsigned	factorial (unsigned n)
	calculate the factorial of an integer More...
PetscInt	get_D_Coeffs (const PetscScalar s[], const PetscInt &n, Vec &output, const PetscInt &d=2)
	Solve arbitrary stencil points s of length N with order of derivatives d<N can be obtained from equation on MIT website http://web.media.mit.edu/~crtaylor/calculator.html where the accuracy is determined as the usual form O(h^(N-d)) More...
int	Init_Mat (Mat &A, const PetscInt &n)
	Initialize a Matrix A to be of size nxn. More...
int	Init_Mat (Mat &A, const PetscInt &m, const PetscInt &n)
	Initialize a Matrix A to be of size mxn. More...
int	Init_Vec (Vec &x, const PetscInt &n)
	Initialize a vector x to be of size n. More...
PetscInt	map_D (Mat &output, SPE &data, const PetscInt &n, Vec &yVec, const PetscInt &order=2, const PetscInt &d=2, const PetscBool &periodic=PETSC_FALSE, const PetscBool &staggered=PETSC_FALSE, const PetscBool &reduce_wall_order=PETSC_TRUE)
	map D matrix operator for specified order and derivative, for a non-uniform mesh More...
PetscErrorCode	printScalar (const PetscScalar x[], const PetscInt n=1, char const name[]="x", const PetscViewer viewer=PETSC_VIEWER_STDOUT_WORLD)
	Print PetscScalar variable to screen. More...
PetscErrorCode	printReal (const PetscReal x[], const PetscInt n=1, char const name[]="x", const PetscViewer viewer=PETSC_VIEWER_STDOUT_WORLD)
	Print PetscReal variable to screen. More...
PetscErrorCode	printVec (const Vec &x, const PetscInt n, char const name[]="x")
	Print Vec from PETSc type variable to screen. More...
PetscErrorCode	printInt (const PetscInt x[], const PetscInt n=1, char const name[]="x")
	Print PetscInt variable to screen. More...
void	printVecView (const Vec &x, char const name[]="x viewer", const PetscViewerFormat format=PETSC_VIEWER_DEFAULT)
	view PetscVec variable to screen Open an X-window viewer. Note that we specify the same communicator for the viewer as we used for the distributed vector (PETSC_COMM_WORLD). More...
PetscInt	printMatView (const Mat &A, char const name[]="A viewer", const PetscViewerFormat format=PETSC_VIEWER_DEFAULT)
	view Petsc Mat variable to screen Open an X-window viewer. Note that we specify the same communicator for the viewer as we used for the distributed vector (PETSC_COMM_WORLD). More...
PetscInt	printMatASCII (const Mat &A, char const name[]="printMatASCII.txt", const PetscViewerFormat format=PETSC_VIEWER_DEFAULT)
	view Petsc Mat variable to ASCII file More...
PetscInt	printMatASCII (const Mat &A, std::string name, const PetscViewerFormat format=PETSC_VIEWER_DEFAULT)
	view Petsc Mat variable to ASCII file More...
void	printMatGetDiagonalASCII (const Mat &A, char const name[]="printMatGetDiagonalASCII.txt", const PetscViewerFormat format=PETSC_VIEWER_ASCII_MATLAB)
	print diagonal of Petsc Mat variable to ASCII file More...
void	printVecASCII (const Vec &b, char const name[]="printVecASCII.txt", const PetscViewerFormat format=PETSC_VIEWER_ASCII_MATLAB)
	view Petsc Vec variable to ASCII file More...
PetscErrorCode	printClosureIter (SPE &data)
	print iteration residuals to screen from update_Closure iterations More...
PetscErrorCode	printNonlinearIter (SPE &data)
	print iteration residuals to screen from update_Nonlinear iterations More...
void	printHeaderIter ()
	print iteration residuals header to screen More...
PetscErrorCode	printBaseNonlinearIter (SPE &data, PetscReal basenonlinear_error, PetscInt basenonlinear_iter)
	print iteration residuals to screen from baseflow nonlinear iterations More...
int	Read_input_file (SPE &data, char const buff[]="input_file.json")
	Read an input file written in json format. More...
int	set_input_value (Json::Value &val, const char buff[], PetscInt &v)
	take Json data and save it to value if it exists More...
int	set_input_value (Json::Value &val, const char buff[], PetscReal &v)
	take Json data and save it to value if it exists More...
int	set_input_value (Json::Value &val, const char buff[], PetscScalar &v)
	take Json data and save it to value if it exists More...
int	set_input_value (Json::Value &val, const char buff[], PetscBool &v)
	take Json data and save it to value if it exists More...
int	set_input_value (Json::Value &val, const char buff[], char *v)
	take Json data and save it to value if it exists More...
int	set_input_value (Json::Value &val, const char buff[], std::string &v)
	take Json data and save it to value if it exists More...
int	Read_q (SPE &data, std::string &buff)
	Read q from a tofile output from python. More...
int	Read_q (Vec &output, const int n, std::string &buff)
	Read q from a tofile output from python. More...
int	Read_q (PetscScalar output[], const int n, std::string &buff)
	Read y from a tofile output from python. More...
int	Read_q (PetscScalar &output, std::string &buff)
	Read complex scalar from a tofile output from python. More...
PetscErrorCode	Read_MatLabVec (Vec &output, std::string &buff)
	Read complex scalar vector from a matlab file (be sure this uses the PetscBinaryWrite() MatLab function) More...
PetscErrorCode	Read_MatLabMat (Mat &output, std::string &buff)
	Read complex scalar matrix from a matlab file (be sure this uses the PetscBinaryWrite() MatLab function) More...
PetscErrorCode	Read_MatLab (SPE &data, std::string &buff)
	Read input matrix and vectors input data from a matlab files (be sure this uses the PetscBinaryWrite() MatLab function) Reads and sets y, yVec, z, zVec, q, qp1, alpha, Deltay, and Deltaz quantities in the SPE class. More...
PetscInt	set_A_and_B_OSS_zi (SPE &data, const PetscInt &zi=0)
	set A and B matrix for Orr-Sommerfeld equations for zi plane Note that the wavelike ansatz is \(u=\hat{u}(y,z) \exp (i (-\omega t + \alpha x))\) \[ \begin{aligned} (-i \omega - \frac{1}{Re}(\partial_y^2 + \partial_z^2))\hat{u} + U' \hat{v} &= \alpha (-i \hat{P} - \frac{i}{Re}(\partial_y \hat{v} + \partial_z \hat{w}) - iU \hat{u})\\ (-i \omega - \frac{1}{Re}(\partial_y^2 + \partial_z^2))\hat{v} + \partial_y \hat{P} &= \alpha (- \frac{1}{Re}(\alpha \hat{v}) - iU \hat{v})\\ (\alpha \hat{v}) &= \alpha \cdot \hat{v}\\ (-i \omega - \frac{1}{Re}(\partial_y^2 + \partial_z^2))\hat{w} + \partial_z \hat{P} &= \alpha (- \frac{1}{Re}(\alpha \hat{w}) - iU \hat{w})\\ (\alpha \hat{w}) &= \alpha \cdot \hat{w}\\ \partial_y \hat{v} + \partial_z \hat{w} &= \alpha (-i \hat{u})\\ \end{aligned}\] Where we have \[ \begin{aligned} \mathbf{z}_i= \begin{bmatrix} \hat{u}\\ \alpha \hat{v}\\ \hat{v}\\ \alpha \hat{w}\\ \hat{w}\\ \hat{P} \end{bmatrix}_{z=z(i)} \textrm{ and } & \mathbf{q} = \begin{bmatrix} \mathbf{z}_1\\ \mathbf{z}_2\\ \vdots \\ \mathbf{z}_{nz - 1}\\ \mathbf{z}_{nz}\\ \end{bmatrix}\\ \end{aligned}\] To solve the spatial eigenvalue problem \(\mathbf{\mathcal{A}q} = \alpha \mathbf{\mathcal{B}q}\) More...
PetscInt	set_A_and_Ds (SPE &data, PetscScalar &alpha)
	set A and B matrix for SPE equations More...
PetscInt	set_A_and_Ds (SPE &data)
	set A and B matrix for SPE equations, this is called from set_A_and_Ds(data,alplha) function This is used to set the full 3D operators (y,z, and t) More...
PetscInt	set_A_and_Ds_nonlinear (SPE &data)
	set A and D matrix linear terms for SPE equations for nonlinear terms More...
PetscInt	set_A_and_Ds_zi (SPE &data, PetscScalar &alpha, const PetscInt &zi=0)
	set A and B matrix linear terms for SPE equations for zi plane (also sets the permutation matrices to extract u from q, etc. More...
PetscInt	set_b (const Mat &B, const Vec &qn, Vec &b)
	set b vector from B and q as b=B*q More...
PetscInt	set_BCs (Mat &A, Vec &b, const PetscInt &ny, const PetscInt &nz)
	sets Boundary Condition equations in Matrix A and vector b in Ax=b linear system for solving the SPE equations More...
PetscInt	set_BCs (SPE &data)
	sets Boundary Condition equations in Matrix A and Matrix B in A+ B*dqdx=0 linear system for solving the SPE equations More...
PetscInt	set_Crank_Nicolson_Advance (SPE &data, Vec &q, PetscScalar &alpha)
	set up Crank-Nicolson advancing matrices A x = b system by creating matrices and setting BCs More...
PetscInt	set_D (const PetscScalar y[], const PetscScalar yP[], const PetscInt &n, Mat &output, SPE &data, const PetscInt &order=2, const PetscInt &d=2, const PetscBool &periodic=PETSC_FALSE, const PetscBool &staggered=PETSC_FALSE, const PetscBool &reduce_wall_order=PETSC_TRUE, const PetscBool &uniform=PETSC_TRUE)
	set D matrix operator for specified order and derivative More...
PetscInt	set_D_fourier (const PetscInt N, const PetscScalar &T, Mat &output, const PetscInt &d=1)
	set D matrix operator for specified derivative using fouier collocated points More...
PetscInt	set_D (SPE &data)
	set D matrices and operators for use in OSS and SPE More...
PetscInt	set_Euler_Advance (SPE &data, Vec &q, PetscScalar &alpha)
	set up Euler advancing matrices A x = b system by creating matrices and setting BCs More...
PetscInt	set_Mat (const PetscScalar *const *Ain, const PetscInt &n, Mat &A, const InsertMode &addv=ADD_VALUES)
	set a matrix from PetscScalar 2D matrix to PETSc Mat type in parallel More...
PetscInt	set_Mat (const PetscScalar &diag, const PetscInt &n, Mat &A, const PetscInt &k=0, const PetscBool &parallel=PETSC_TRUE, const InsertMode &addv=ADD_VALUES)
	set a diagonal of a matrix from scalar More...
PetscInt	set_Mat (Mat &A)
	Assemble matrix. More...
PetscInt	set_Mat (const PetscScalar &value, const PetscInt &row, const PetscInt &col, Mat &A, const PetscBool &parallel=PETSC_TRUE, const InsertMode &addv=ADD_VALUES)
	set a single value in matrix at row,col More...
PetscInt	set_Mat (const PetscScalar &a, const Mat &Asub, const PetscInt &nsub, Mat &A, const PetscInt &n, const PetscInt &rowoffset=0, const PetscInt &coloffset=0, const InsertMode &addv=ADD_VALUES)
	set a submatrix Asub in a matrix A More...
PetscInt	set_Mat (const PetscScalar *Ain, const PetscInt &row, const PetscInt &ncols, const PetscInt cols[], Mat &A, const InsertMode &addv=ADD_VALUES)
	set a row of PetscScalar to a matrix to PETSc Mat More...
PetscInt	set_Mat (const PetscScalar &a, const Mat &Dz, const PetscInt &nz, const PetscInt &ny, const PetscInt &zi, Mat &A, const PetscInt &n, const PetscInt &nvars=4, const PetscInt &rowoffset=0, const PetscInt &coloffset=0, const InsertMode &addv=ADD_VALUES)
	set a Dz submatrix into A More...
PetscInt	set_MatDiagonalScale (const Mat &diag_to_scale, const Mat &Asub, const PetscInt &nsub, Mat &A, const PetscInt &n, const PetscInt &rowoffset=0, const PetscInt &coloffset=0, const InsertMode &addv=ADD_VALUES)
	set a scaled matrix, (rows are scaled by matrix, using A=LA and MatDiagonalScale) More...
PetscInt	set_Mat_broadcast_from_colVec (Vec &x, PetscInt &n, Mat &A)
	set a matrix from a column vector (broadcast the column vector to all columns of a matrix Be sure that A is already initialized More...
PetscInt	set_Mat_from_Vec (Vec &x, PetscInt &ny, PetscInt &nz, PetscInt &rowoffset, Mat &A, const InsertMode &addv=ADD_VALUES)
	set a matrix A (large ny*nz*4) from a vector (ny*nz) (used in the diagonals) at a certain rowoffset (between 0-ny*3). Be sure that A is already initialized More...
PetscInt	set_Mat_kron (const Mat &A, const Mat &B, Mat &C)
	Kronecker tensor product of two matrices A and B to make C If A is m by n, and B is p by q, then C will be m*p by n*q matrix formed by taking all possible products between the elements of A and the matrix B. See wikipedia for more information here. More...
PetscInt	set_Mat_aPDdim_to_A (PetscScalar a, Mat &P, Mat &D, Mat &A)
PetscInt	set_P (SPE &data)
	set permutation matrices and operators for use in OSS and SPE More...
PetscInt	set_Vec (const PetscScalar *bin, const PetscInt &n, Vec &b, const PetscBool &parallel=PETSC_TRUE)
	set a vector from PetscScalar 1D vector to PETSc Vec type in parallel More...
PetscInt	set_Vec (Vec &b)
	Assemble b vector. More...
PetscInt	set_Vec (const PetscScalar &bin, const PetscInt &n, Vec &b)
	set a vector from PetscScalar to PETSc Vec in location n More...
PetscInt	set_Vec (const Vec &inVec, const PetscInt &low, const PetscInt &hi, Vec &b)
	set a subvector from larger vector from low to hi indices More...
PetscInt	set_Vec_linspace (PetscScalar a, const PetscScalar b, const PetscInt n, PetscScalar y[])
	set values of y, use linspace similar to matlab, creates on every processor More...
int	trapz (const Vec &q, PetscScalar &I, SPE &data)
	trapezoidal rule on Vec with ny,nz values More...
PetscErrorCode	trapz_4nynznt (const Vec &q, PetscScalar &I, SPE &data)
	trapezoidal rule on Vec with 4,ny,nz,nt values More...
int	update_Closure (SPE &data, Vec &q, Vec &qp1, PetscScalar &alpha, const PetscInt &maxiter=50)
	calculate the closure equation \( \int_\Omega \hat{\textbf{q}}^\dagger \hat{\textbf{q}}_x dy \) and output the result This is part of the solution procedure shown in the bottom half of this diagram More...
int	update_Nonlinear (SPE &data, Vec &q, Vec &qp1, PetscScalar &alpha_old, PetscScalar &alpha, PetscScalar &Ialpha_old, PetscScalar &Ialpha, const PetscInt &maxiter=50)
	advance the Nonlinear SPE system one x step More...

Detailed Description

Namespace containing all functions and data classes for this solver.

Function Documentation

int SPE::_bblf	(	const PetscScalar	input[3],
		PetscScalar	output[3]
	)

Blasius boundary layer function to integrate. Similarity Blasius ODE broken into three coupled equations

\[ \begin{aligned} f'' &= \int -ff'' d\eta\\ f' &= \int f'' d\eta\\ f &= \int f' d\eta\\ \end{aligned} \]

.

Parameters

[in]	input	\([f'', f', f]^T\) state at \( \eta_i \)
[out]	output	\([f'', f', f]^T\) state at \(\eta_{i+1} \)

PetscInt SPE::Ax_b	(	const PetscScalar *const *	Ain,
		Vec &	x,
		const PetscScalar	bin[],
		const PetscInt &	n
	)

Solves \(x\) in \(Ax=b\) linalg problem using PETSc in parallel Useful for solving small systems of equations, such as finite difference coefficients for given stencils.

Returns

0 if successful

Parameters

[in]	Ain	input of 2D \(A\) matrix in \(Ax=b\) (must be dynamic pointer to pointer)
[in,out]	x	vector of \(x\) in \(Ax=b\) (already initialized)
[in]	bin	vector of \(b\) in \(Ax=b\)
[in]	n	n size of vectors or nxn matrix \(A\)

PetscInt SPE::Ax_b	(	const Mat &	A,
		Vec &	x,
		const Vec &	b,
		const PetscInt &	n
	)

Solves \(x\) in \(Ax=b\) linalg problem using PETSc in parallel.

Returns

0 if successful

Parameters

[in]	A	input of A matrix in \(Ax=b\)
[in,out]	x	vector of \(x\) in \(Ax=b\) (already initialized)
[in]	b	vector of \(b\) in \(Ax=b\)
[in]	n	n size of vectors or nxn matrix \(A\)

PetscInt SPE::Ax_kBx	(	const Mat &	A,
		const Mat &	B,
		PetscScalar &	kr,
		PetscScalar &	ki,
		Vec &	xr,
		Vec &	xi,
		PetscScalar	target = 0.54213+0.082968*PETSC_i,
		PetscInt	nev = 1,
		EPSWhich	which = EPS_TARGET_MAGNITUDE
	)

Solves \(x\) in \(Ax=kBx\) eigenvalue problem using SLEPc in parallel.

Returns

0 if successful

Parameters

[in]	A	input of A matrix in \(Ax=kBx\)
[in]	B	input of B matrix in \(Ax=kBx\)
[out]	kr	real part of eigenvalue
[out]	ki	imag part of eigenvalue
[out]	xr	vector of \(x\) in \(Ax=kBx\) (already initialized)
[out]	xi	vector of \(x\) in \(Ax=kBx\) (already initialized)
[in]	target	target eigenvalue to solve around using the which parameter
[in]	nev	number of eigenvalues to compute
[in]	which	portion of spectrum to be sought

int SPE::base_flow

(

SPE &

data

)

set plane channel or blasius boundary layer flow velocity variables \(U, U_x, U_y,\) and etc Note: type_base_flow has an integer flag that corresponds with the following flow types

• 1 - Poisuille channel flow
• 2 - Blasius Flat-Plate
• 3 - SPE Boundary Layer equations with nonlinear forcing terms for Mean Flow Distortion
• 4 - Read U,V,P from DNS data set located in the file sets of read_matlab_filename + "_Base_Flow/Base_Flow_istep_%i.dat"
• 5 - SPE Boundary Layer equations with nonlinear forcing terms for Mean Flow Distortion for semi-staggered grid use this once to set the vectors with the velocity of plane channel flow (max u=1)

  Returns

  0 if successful

Parameters

[in,out]

data

data from class passed in and out

int SPE::base_flow_dim

(

SPE &

data

)

Use this after base_flow(data) call to set the ny matrices to size dim. So U is set into U_dim.

Returns

0 if successful

Parameters

[in,out]

data

data from class passed in and out

int SPE::calc_Closure	(	PetscScalar &	I,
		SPE &	data,
		Vec &	q,
		Vec &	qp1
	)

calculate the closure equation \( \int_{\Omega} \hat{\textbf{q}}^\dagger \hat{\textbf{q}}_x d\Omega \) and output the result

Returns

0 if successful

Parameters

[out]	I	output integral value
[in,out]	data	data class to store values
[in]	q	q at last marching step
[in]	qp1	q at current marching step

int SPE::calc_L2	(	PetscReal &	error,
		Vec &	x1,
		Vec &	x2,
		PetscInt	n,
		NormType	type = NORM_2
	)

calculate the \( L_2 \) norm of the difference between \(x_1\) and \(x_2\) vectors and return

Returns

0 if successful

Parameters

[out]	error	\(L_2\) norm of the difference between \(x_1\) and \(x_2\) vectors
[in]	x1	\(x_1\) vector
[in]	x2	\(x_2\) vector
[in]	n	size of vectors
[in]	type	type of norm (default NORM_2 \(\sqrt{\sum |x_1-x_2|^2}\)

int SPE::calc_L2	(	PetscReal &	error,
		Mat &	x1,
		Mat &	x2,
		PetscInt	n,
		NormType	type = NORM_2
	)

calculate the \( L_2 \) norm of the difference between \(x_1\) and \(x_2\) matrix diagonals and return

Returns

0 if successful

Parameters

[out]	error	\(L_2\) norm of the difference between \(x_1\) and \(x_2\) vectors
[in]	x1	\(x_1\) diagonal matrix
[in]	x2	\(x_2\) diagonal matrix
[in]	n	size of vectors
[in]	type	type of norm (default NORM_2 \(\sqrt{\sum |x_1-x_2|^2}\)

int SPE::calc_LST	(	SPE &	data,
		PetscScalar	target_alpha,
		PetscScalar &	alpha,
		Vec &	qp1_OSS,
		Vec &	qp1
	)

calculate the Local Stability Theory (LST) Orr-Sommerfeld Squire equations in primitive variables at this x-location and store the alpha and qp1 of the target spatial values.

See also

set_A_and_B_OSS_zi.hpp

Returns

0 if successful

Parameters

[in,out]	data	data class to store values
[in]	target_alpha	target alpha guess
[out]	alpha	alpha from OSS solver
[out]	qp1_OSS	eigenvector of size data.dimOSS
[out]	qp1	eigenvector of size data.dim

int SPE::Create_grid	(	SPE &	data,
		PetscScalar	deltay = 0.
	)

create y and z grid and stretch in y direction using stretching if deltay is nonzero

Returns

0 if successful

Parameters

[in,out]	data	data class to hold data
[in]	deltay	stretching in y direction using hyperbolic stretching function

unsigned SPE::factorial

(

unsigned

n

)

calculate the factorial of an integer

Returns

n!

Parameters

[out]

n

input integer to perform factorial on

PetscInt SPE::get_D_Coeffs	(	const PetscScalar	s[],
		const PetscInt &	n,
		Vec &	output,
		const PetscInt &	d = 2
	)

Solve arbitrary stencil points s of length N with order of derivatives d<N can be obtained from equation on MIT website http://web.media.mit.edu/~crtaylor/calculator.html where the accuracy is determined as the usual form O(h^(N-d))

ierr from Ax=b solver

Parameters

[in]	s	array of stencil points e.g. [-3,-2,-1,0,1]
[in]	n	size of stencil
[out]	output	output of coefficient values for the given stencil (uninitialized)
[in]	d	order of desired derivative (default=2)

int SPE::Init_Mat	(	Mat &	A,
		const PetscInt &	n
	)

Initialize a Matrix A to be of size nxn.

Returns

0 if successful

Parameters

[out]	A	A matrix to initialize in MPI (uninitialized)
[in]	n	number of global rows and columns

int SPE::Init_Mat	(	Mat &	A,
		const PetscInt &	m,
		const PetscInt &	n
	)

Initialize a Matrix A to be of size mxn.

Returns

0 if successful

Parameters

[out]	A	A matrix to initialize in MPI (uninitialized)
[in]	m	number of global rows
[in]	n	number of global columns

int SPE::Init_Vec	(	Vec &	x,
		const PetscInt &	n
	)

Initialize a vector x to be of size n.

Returns

0 if successful

Parameters

[out]	x	x vector to initialize in MPI (uninitialized)
[in]	n	size of vector

PetscInt SPE::map_D	(	Mat &	output,
		SPE &	data,
		const PetscInt &	n,
		Vec &	yVec,
		const PetscInt &	order = 2,
		const PetscInt &	d = 2,
		const PetscBool &	periodic = PETSC_FALSE,
		const PetscBool &	staggered = PETSC_FALSE,
		const PetscBool &	reduce_wall_order = PETSC_TRUE
	)

map D matrix operator for specified order and derivative, for a non-uniform mesh

Returns

0 if successful

Parameters

[in,out]	output	matrix(n by n) dth derivative of order O(h^order) assuming uniform xi spacing coming in (initialized), then output a non-uniform derivative w.r.t. y
[in]	data	data class to have flags
[in]	n	length of y values
[in]	yVec	y non-uniform data pts of interest
[in]	order	order of accuracy desired (assuming even e.g. 2,4,6,...)
[in]	d	dth derivative
[in]	periodic	periodic boundary
[in]	staggered	if setting staggered pressure derivative
[in]	reduce_wall_order	reduce the order of accuracy at the wall?

PetscErrorCode SPE::printBaseNonlinearIter	(	SPE &	data,
		PetscReal	basenonlinear_error,
		PetscInt	basenonlinear_iter
	)

print iteration residuals to screen from baseflow nonlinear iterations

Parameters

[in]	data	data class storing iterations and residual values
[in]	basenonlinear_error	nonlinear error for the baseflow
[in]	basenonlinear_iter	base flow nonlinear iteration

PetscErrorCode SPE::printClosureIter

(

SPE &

data

)

print iteration residuals to screen from update_Closure iterations

Parameters

[in]

data

data class storing iterations and residual values

void SPE::printHeaderIter

(

)

print iteration residuals header to screen

PetscErrorCode SPE::printInt	(	const PetscInt	x[],
		const PetscInt	n = 1,
		char const	name[] = "x"
	)

Print PetscInt variable to screen.

Returns

ierr from PetscErrorCode of PetscPrintf

Parameters

[in]	x	PetscScalar array to print to screen
[in]	n	size of scalar array to print
[in]	name	name of variable to output default to 'x'

PetscInt SPE::printMatASCII	(	const Mat &	A,
		char const	name[] = "printMatASCII.txt",
		const PetscViewerFormat	format = PETSC_VIEWER_DEFAULT
	)

view Petsc Mat variable to ASCII file

• Helpful runtime option:

-draw_pause <pause> : sets time (in seconds) that the program pauses after PetscDrawPause() has been called (0 is default, -1 implies until user input).

Parameters

[in]	A	Petsc Mat nxn matrix to print to screen
[in]	name	filename to write to
[in]	format	format for viewer

PetscInt SPE::printMatASCII	(	const Mat &	A,
		std::string	name,
		const PetscViewerFormat	format = PETSC_VIEWER_DEFAULT
	)

view Petsc Mat variable to ASCII file

• Helpful runtime option:

-draw_pause <pause> : sets time (in seconds) that the program pauses after PetscDrawPause() has been called (0 is default, -1 implies until user input).

Parameters

[in]	A	Petsc Mat nxn matrix to print to screen
[in]	name	filename to write to
[in]	format	format for viewer

void SPE::printMatGetDiagonalASCII	(	const Mat &	A,
		char const	name[] = "printMatGetDiagonalASCII.txt",
		const PetscViewerFormat	format = PETSC_VIEWER_ASCII_MATLAB
	)

print diagonal of Petsc Mat variable to ASCII file

• Helpful runtime option:

-draw_pause <pause> : sets time (in seconds) that the program pauses after PetscDrawPause() has been called (0 is default, -1 implies until user input).

Parameters

[in]	A	Petsc Mat nxn matrix to print to screen
[in]	name	filename to write to
[in]	format	format for viewer

PetscInt SPE::printMatView	(	const Mat &	A,
		char const	name[] = "A viewer",
		const PetscViewerFormat	format = PETSC_VIEWER_DEFAULT
	)

view Petsc Mat variable to screen Open an X-window viewer. Note that we specify the same communicator for the viewer as we used for the distributed vector (PETSC_COMM_WORLD).

• Helpful runtime option:

-draw_pause <pause> : sets time (in seconds) that the program pauses after PetscDrawPause() has been called (0 is default, -1 implies until user input).

Parameters

[in]	A	Petsc Mat nxn matrix to print to screen
[in]	name	name of variable to output default to 'A'
[in]	format	format for viewer

PetscErrorCode SPE::printNonlinearIter

(

SPE &

data

)

print iteration residuals to screen from update_Nonlinear iterations

Parameters

[in]

data

data class storing iterations and residual values

PetscErrorCode SPE::printReal	(	const PetscReal	x[],
		const PetscInt	n = 1,
		char const	name[] = "x",
		const PetscViewer	viewer = PETSC_VIEWER_STDOUT_WORLD
	)

Print PetscReal variable to screen.

Returns

ierr from PetscErrorCode of PetscPrintf

Parameters

[in]	x	PetscReal array to print to screen
[in]	n	size of scalar array to print
[in]	name	name of variable to output default to 'x'
[in]	viewer	format for viewer

PetscErrorCode SPE::printScalar	(	const PetscScalar	x[],
		const PetscInt	n = 1,
		char const	name[] = "x",
		const PetscViewer	viewer = PETSC_VIEWER_STDOUT_WORLD
	)

Print PetscScalar variable to screen.

Returns

ierr from PetscErrorCode of PetscPrintf

Parameters

[in]	x	PetscScalar array to print to screen
[in]	n	size of scalar array to print
[in]	name	name of variable to output default to 'x'
[in]	viewer	format for viewer

PetscErrorCode SPE::printVec	(	const Vec &	x,
		const PetscInt	n,
		char const	name[] = "x"
	)

Print Vec from PETSc type variable to screen.

Returns

ierr from PetscErrorCode of PetscPrintf

Parameters

[in]	x	Vec array to print to screen
[in]	n	size of scalar array to print
[in]	name	name of variable to output default to 'x'

void SPE::printVecASCII	(	const Vec &	b,
		char const	name[] = "printVecASCII.txt",
		const PetscViewerFormat	format = PETSC_VIEWER_ASCII_MATLAB
	)

view Petsc Vec variable to ASCII file

• Helpful runtime option:

-draw_pause <pause> : sets time (in seconds) that the program pauses after PetscDrawPause() has been called (0 is default, -1 implies until user input).

Parameters

[in]	b	Petsc Vec 1xn vector to print to screen
[in]	name	filename to write to
[in]	format	format for viewer

void SPE::printVecView	(	const Vec &	x,
		char const	name[] = "x viewer",
		const PetscViewerFormat	format = PETSC_VIEWER_DEFAULT
	)

view PetscVec variable to screen Open an X-window viewer. Note that we specify the same communicator for the viewer as we used for the distributed vector (PETSC_COMM_WORLD).

• Helpful runtime option:

-draw_pause <pause> : sets time (in seconds) that the program pauses after PetscDrawPause() has been called (0 is default, -1 implies until user input).

Parameters

[in]	x	PetscScalar array to print to screen
[in]	name	name of variable to output default to 'x'
[in]	format	format for viewer

int SPE::Read_input_file	(	SPE &	data,
		char const	buff[] = "input_file.json"
	)

Read an input file written in json format.

Returns

0 if successful

Parameters

[in,out]	data	data class to hold data
[in]	buff	filename of binary to read (output of python script

int SPE::Read_MatLab	(	SPE &	data,
		std::string &	buff
	)

Read input matrix and vectors input data from a matlab files (be sure this uses the PetscBinaryWrite() MatLab function) Reads and sets y, yVec, z, zVec, q, qp1, alpha, Deltay, and Deltaz quantities in the SPE class.

Returns

ierr

Parameters

[in,out]	data	data class to hold data
[in]	buff	filename (without endings) of binary matlab files to read (output of matlab script using PetscSpecific binary write functions and fwrite)

PetscErrorCode SPE::Read_MatLabMat	(	Mat &	output,
		std::string &	buff
	)

Read complex scalar matrix from a matlab file (be sure this uses the PetscBinaryWrite() MatLab function)

Returns

ierr

Parameters

[out]	output	complex scalar matrix to return after reading file (uninitialized)
[in]	buff	filename of binary matlab file to read (output of matlab script using PetscSpecific binary write functions)

PetscErrorCode SPE::Read_MatLabVec	(	Vec &	output,
		std::string &	buff
	)

Read complex scalar vector from a matlab file (be sure this uses the PetscBinaryWrite() MatLab function)

Returns

ierr

Parameters

[out]	output	complex scalar vector to return after reading file (uninitialized)
[in]	buff	filename of binary matlab file to read (output of matlab script using PetscSpecific binary write functions)

int SPE::Read_q	(	SPE &	data,
		std::string &	buff
	)

Read q from a tofile output from python.

Returns

0 if successful

Parameters

[in,out]	data	data class to hold data
[in]	buff	filename of binary to read (output of python script)

int SPE::Read_q	(	Vec &	output,
		const int	n,
		std::string &	buff
	)

Read q from a tofile output from python.

Returns

0 if successful

Parameters

[in,out]	output	vector to return after reading file (already initialized)
[in]	n	int size of vector
[in]	buff	filename of binary to read (output of python script)

int SPE::Read_q	(	PetscScalar	output[],
		const int	n,
		std::string &	buff
	)

Read y from a tofile output from python.

Returns

0 if successful

Parameters

[out]	output	vector to return after reading file
[in]	n	int size of vector
[in]	buff	filename of binary to read (output of python script)

int SPE::Read_q	(	PetscScalar &	output,
		std::string &	buff
	)

Read complex scalar from a tofile output from python.

Returns

0 if successful

Parameters

[out]	output	complex scalar to return after reading file
[in]	buff	filename of binary to read (output of python script)

PetscInt SPE::set_A_and_B_OSS_zi	(	SPE &	data,
		const PetscInt &	zi = 0
	)

set A and B matrix for Orr-Sommerfeld equations for zi plane Note that the wavelike ansatz is \(u=\hat{u}(y,z) \exp (i (-\omega t + \alpha x))\)

\[ \begin{aligned} (-i \omega - \frac{1}{Re}(\partial_y^2 + \partial_z^2))\hat{u} + U' \hat{v} &= \alpha (-i \hat{P} - \frac{i}{Re}(\partial_y \hat{v} + \partial_z \hat{w}) - iU \hat{u})\\ (-i \omega - \frac{1}{Re}(\partial_y^2 + \partial_z^2))\hat{v} + \partial_y \hat{P} &= \alpha (- \frac{1}{Re}(\alpha \hat{v}) - iU \hat{v})\\ (\alpha \hat{v}) &= \alpha \cdot \hat{v}\\ (-i \omega - \frac{1}{Re}(\partial_y^2 + \partial_z^2))\hat{w} + \partial_z \hat{P} &= \alpha (- \frac{1}{Re}(\alpha \hat{w}) - iU \hat{w})\\ (\alpha \hat{w}) &= \alpha \cdot \hat{w}\\ \partial_y \hat{v} + \partial_z \hat{w} &= \alpha (-i \hat{u})\\ \end{aligned}\]

Where we have

\[ \begin{aligned} \mathbf{z}_i= \begin{bmatrix} \hat{u}\\ \alpha \hat{v}\\ \hat{v}\\ \alpha \hat{w}\\ \hat{w}\\ \hat{P} \end{bmatrix}_{z=z(i)} \textrm{ and } & \mathbf{q} = \begin{bmatrix} \mathbf{z}_1\\ \mathbf{z}_2\\ \vdots \\ \mathbf{z}_{nz - 1}\\ \mathbf{z}_{nz}\\ \end{bmatrix}\\ \end{aligned}\]

To solve the spatial eigenvalue problem \(\mathbf{\mathcal{A}q} = \alpha \mathbf{\mathcal{B}q}\)

Returns

0 if successful

Parameters

[in,out]	data	data class to store values
[in]	zi	zi plane of matrix

PetscInt SPE::set_A_and_Ds	(	SPE &	data,
		PetscScalar &	alpha
	)

set A and B matrix for SPE equations

Returns

0 if successful

Parameters

[in,out]	data	data class containing all matrices, vectors, scalars, and problem size
[in]	alpha	\( \alpha \) eigenvalue from previous iteration

PetscInt SPE::set_A_and_Ds

(

SPE &

data

)

set A and B matrix for SPE equations, this is called from set_A_and_Ds(data,alplha) function This is used to set the full 3D operators (y,z, and t)

Returns

0 if successful

Parameters

[in,out]

data

data class containing all matrices, vectors, scalars, and problem size

PetscInt SPE::set_A_and_Ds_nonlinear

(

SPE &

data

)

set A and D matrix linear terms for SPE equations for nonlinear terms

Returns

0 if successful

Parameters

[in,out]

data

data class to store values

PetscInt SPE::set_A_and_Ds_zi	(	SPE &	data,
		PetscScalar &	alpha,
		const PetscInt &	zi = 0
	)

set A and B matrix linear terms for SPE equations for zi plane (also sets the permutation matrices to extract u from q, etc.

Returns

0 if successful

Parameters

[in,out]	data	data class to store values
[in]	alpha	eigenvalue from previous iteration
[in]	zi	zi plane of matrix

PetscInt SPE::set_b	(	const Mat &	B,
		const Vec &	qn,
		Vec &	b
	)

set b vector from B and q as b=B*q

Returns

0 if successful

Parameters

[in]	B	B matrix
[in]	qn	qn vector to multiply
[in,out]	b	b Vec (already initialized)

PetscInt SPE::set_BCs	(	Mat &	A,
		Vec &	b,
		const PetscInt &	ny,
		const PetscInt &	nz
	)

sets Boundary Condition equations in Matrix A and vector b in Ax=b linear system for solving the SPE equations

Returns

0 if successful

Parameters

[in,out]	A	A matrix (already initialized)
[in,out]	b	b Vec (already initialized)
[in]	ny	size of y array
[in]	nz	size of z array

PetscInt SPE::set_BCs

(

SPE &

data

)

sets Boundary Condition equations in Matrix A and Matrix B in A+ B*dqdx=0 linear system for solving the SPE equations

Returns

0 if successful

Parameters

[in]

data

data class for flags

PetscInt SPE::set_Crank_Nicolson_Advance	(	SPE &	data,
		Vec &	q,
		PetscScalar &	alpha
	)

set up Crank-Nicolson advancing matrices A x = b system by creating matrices and setting BCs

Returns

0 if successful

Parameters

[in,out]	data	data class to store values
[in]	q	q at last marching step
[in]	alpha	eigenvalue from previous step

PetscInt SPE::set_D	(	const PetscScalar	y[],
		const PetscScalar	yP[],
		const PetscInt &	n,
		Mat &	output,
		SPE &	data,
		const PetscInt &	order = 2,
		const PetscInt &	d = 2,
		const PetscBool &	periodic = PETSC_FALSE,
		const PetscBool &	staggered = PETSC_FALSE,
		const PetscBool &	reduce_wall_order = PETSC_TRUE,
		const PetscBool &	uniform = PETSC_TRUE
	)

set D matrix operator for specified order and derivative

Returns

0 if successful

if odd derivative

if odd derivative

if odd derivative

if odd derivative

Parameters

[in]	y	array of y values
[in]	yP	array of y values of semi-staggered pressure locations (size ny-1)
[in]	n	length of y values
[out]	output	matrix(n by n) dth derivative of order O(h^order) assuming uniform y spacing (uninitialized)
[in]	data	data class to have flags
[in]	order	order of accuracy desired (assuming even e.g. 2,4,6,...) (default 2)
[in]	d	dth derivative (default 2)
[in]	periodic	periodic boundary (default false)
[in]	staggered	if setting staggered pressure derivative (default false)
[in]	reduce_wall_order	reduce the order of accuracy at the wall? (default true)
[in]	uniform	uniform mesh? (default true)

PetscInt SPE::set_D

(

SPE &

data

)

set D matrices and operators for use in OSS and SPE

Returns

0 if successful

Parameters

[in]

data

data class to have flags

PetscInt SPE::SPE::set_D_fourier	(	const PetscInt	N,
		const PetscScalar &	T,
		Mat &	output,
		const PetscInt &	d = 1
	)

set D matrix operator for specified derivative using fouier collocated points

Returns

0 if successful

Parameters

[in]	N	length of collocated points
[in]	T	period of y values
[out]	output	matrix(n by n) dth derivative of order O(h^order) assuming uniform y spacing (uninitialized)
[in]	d	dth derivative (default 1)

PetscInt SPE::set_Euler_Advance	(	SPE &	data,
		Vec &	q,
		PetscScalar &	alpha
	)

set up Euler advancing matrices A x = b system by creating matrices and setting BCs

Returns

0 if successful

Parameters

[in,out]	data	data class to store values
[in]	q	q at last marching step
[in]	alpha	eigenvalue \( \alpha \) from the previous iteration

int SPE::set_input_value	(	Json::Value &	val,
		const char	buff[],
		PetscInt &	v
	)

take Json data and save it to value if it exists

Returns

0 if successful

Parameters

val	Json file after reading
buff	matching key to check if it exits, if it does, set the value
v	value to set if key is matching

int SPE::set_input_value	(	Json::Value &	val,
		const char	buff[],
		PetscReal &	v
	)

take Json data and save it to value if it exists

Returns

0 if successful

Parameters

val	Json file after reading
buff	matching key to check if it exits, if it does, set the value
v	value to set if key is matching

int SPE::set_input_value	(	Json::Value &	val,
		const char	buff[],
		PetscScalar &	v
	)

take Json data and save it to value if it exists

Returns

0 if successful

Parameters

val	Json file after reading
buff	matching key to check if it exits, if it does, set the value
v	value to set if key is matching

int SPE::set_input_value	(	Json::Value &	val,
		const char	buff[],
		PetscBool &	v
	)

take Json data and save it to value if it exists

Returns

0 if successful

Parameters

val	Json file after reading
buff	matching key to check if it exits, if it does, set the value
v	value to set if key is matching

int SPE::set_input_value	(	Json::Value &	val,
		const char	buff[],
		char *	v
	)

take Json data and save it to value if it exists

Returns

0 if successful

Parameters

val	Json file after reading
buff	matching key to check if it exits, if it does, set the value
v	value tos et if key is matching (string)

int SPE::set_input_value	(	Json::Value &	val,
		const char	buff[],
		std::string &	v
	)

take Json data and save it to value if it exists

Returns

0 if successful

Parameters

val	Json file after reading
buff	matching key to check if it exits, if it does, set the value
v	value tos et if key is matching (string)

PetscInt SPE::set_Mat	(	const PetscScalar *const *	Ain,
		const PetscInt &	n,
		Mat &	A,
		const InsertMode &	addv = ADD_VALUES
	)

set a matrix from PetscScalar 2D matrix to PETSc Mat type in parallel

Returns

0 if successful

Parameters

[in]	Ain	Matrix set on all processors as 2D array
[in]	n	size of nxn matrix
[out]	A	Mat to SetValues and output in parallel (uninitialized)
[in]	addv	insert values or add values to matrix A

PetscInt SPE::set_Mat	(	const PetscScalar &	diag,
		const PetscInt &	n,
		Mat &	A,
		const PetscInt &	k = 0,
		const PetscBool &	parallel = PETSC_TRUE,
		const InsertMode &	addv = ADD_VALUES
	)

set a diagonal of a matrix from scalar

Returns

0 if successful

Parameters

[in]	diag	scalar value to set as diagonal in matrix
[in]	n	size of nxn matrix
[in,out]	A	Mat to SetValues and output in parallel (already initialized)
[in]	k	diagonal offset in matrix (k=0 is main diagonal, k>0 is above main diagonal, k<0 is below main diagonal) default is 0
[in]	parallel	set the matrix using Istart and Iend
[in]	addv	insert values or add values to matrix A

PetscInt SPE::set_Mat

(

Mat &

A

)

Assemble matrix.

Returns

0 if successful

Parameters

[in,out]

A

Mat to assemble (already initialized)

PetscInt SPE::set_Mat	(	const PetscScalar &	value,
		const PetscInt &	row,
		const PetscInt &	col,
		Mat &	A,
		const PetscBool &	parallel = PETSC_TRUE,
		const InsertMode &	addv = ADD_VALUES
	)

set a single value in matrix at row,col

Returns

0 if successful

Parameters

[in]	value	value to set in Mat A
[in]	row	specified global row in Mat A
[in]	col	specified global col in Mat A
[in,out]	A	Matrix A to set value (already initialized)
[in]	parallel	do this in parallel?
[in]	addv	insert values or add values to matrix A

PetscInt SPE::set_Mat	(	const PetscScalar &	a,
		const Mat &	Asub,
		const PetscInt &	nsub,
		Mat &	A,
		const PetscInt &	n,
		const PetscInt &	rowoffset = 0,
		const PetscInt &	coloffset = 0,
		const InsertMode &	addv = ADD_VALUES
	)

set a submatrix Asub in a matrix A

Returns

0 if successful

Parameters

[in]	a	premultple to Asub
[in]	Asub	sub matrix to set into mat
[in]	nsub	nxn size of square sub matrix Asub
[in,out]	A	Matrix A to set value (already initialized)
[in]	n	size of square Matrix A
[in]	rowoffset	start inserting Asub in A starting at rowoffset row
[in]	coloffset	start inserting Asub in A starting at coloffset column
[in]	addv	insert values or add values to matrix A

PetscInt SPE::set_Mat	(	const PetscScalar *	Ain,
		const PetscInt &	row,
		const PetscInt &	ncols,
		const PetscInt	cols[],
		Mat &	A,
		const InsertMode &	addv = ADD_VALUES
	)

set a row of PetscScalar to a matrix to PETSc Mat

Returns

0 if successful

Parameters

[in]	Ain	array to set in row of matrix
[in]	row	row to set in matrix
[in]	ncols	ncols of array
[in]	cols	cols to set in matrix
[in,out]	A	Mat to SetValues and output in parallel (already initialized)
[in]	addv	insert values or add values to matrix A

PetscInt SPE::set_Mat	(	const PetscScalar &	a,
		const Mat &	Dz,
		const PetscInt &	nz,
		const PetscInt &	ny,
		const PetscInt &	zi,
		Mat &	A,
		const PetscInt &	n,
		const PetscInt &	nvars = 4,
		const PetscInt &	rowoffset = 0,
		const PetscInt &	coloffset = 0,
		const InsertMode &	addv = ADD_VALUES
	)

set a Dz submatrix into A

Returns

0 if successful

Parameters

[in]	a	premultple to Dz
[in]	Dz	sub matrix to set into mat in z direction
[in]	nz	\(n_z \times n_z \) size of square sub matrix Dz
[in]	ny	length of \( y \) array
[in]	zi	which \( z \) plane you are looking at
[in,out]	A	Matrix A to set value (already initialized)
[in]	n	size of square Matrix A
[in]	nvars	number of variables in vector 4 if (u,v,w,P) or 6 if (u, v, av, w, aw, P)
[in]	rowoffset	start inserting Asub in A starting at rowoffset row
[in]	coloffset	start inserting Asub in A starting at coloffset column
[in]	addv	insert values or add values to matrix A

PetscInt SPE::set_Mat_aPDdim_to_A	(	PetscScalar	a,
		Mat &	P,
		Mat &	D,
		Mat &	A
	)

Returns

0 if successful

Parameters

[in]	a	Scalar to multiply Ddim by
[in]	P	Permutation matrix to change block diagonal to fit desired input into A
[in]	D	Derivative matrix (or similar) of size A
[in,out]	A	Matrix that A += a*P (@ is matrix multiply)

PetscInt SPE::set_Mat_broadcast_from_colVec	(	Vec &	x,
		PetscInt &	n,
		Mat &	A
	)

set a matrix from a column vector (broadcast the column vector to all columns of a matrix Be sure that A is already initialized

Returns

0 if successful

Parameters

[in]	x	column Vec
[in]	n	length of Vec
[out]	A	Matrix of size nxn

PetscInt SPE::set_Mat_from_Vec	(	Vec &	x,
		PetscInt &	ny,
		PetscInt &	nz,
		PetscInt &	rowoffset,
		Mat &	A,
		const InsertMode &	addv = ADD_VALUES
	)

set a matrix A (large ny*nz*4) from a vector (ny*nz) (used in the diagonals) at a certain rowoffset (between 0-ny*3). Be sure that A is already initialized

Returns

0 if successful

Parameters

[in]	x	column Vec
[in]	ny	length of Vec is ny*nz
[in]	nz	length of Vec is ny*nz
[in]	rowoffset	start inserting Vec in A starting at rowoffset row
[in,out]	A	Matrix of size ny*nz*4
[in]	addv	insert values or add values to matrix A (default ADD_VALUES)

PetscInt SPE::set_Mat_kron	(	const Mat &	A,
		const Mat &	B,
		Mat &	C
	)

Kronecker tensor product of two matrices A and B to make C If A is m by n, and B is p by q, then C will be m*p by n*q matrix formed by taking all possible products between the elements of A and the matrix B. See wikipedia for more information here.

Returns

0 if successful

Parameters

[in]	A	First matrix \(m \times n\)
[in]	B	Second matrix \(p \times q\)
[out]	C	output matrix \(mp \times n*q\)

PetscInt SPE::set_MatDiagonalScale	(	const Mat &	diag_to_scale,
		const Mat &	Asub,
		const PetscInt &	nsub,
		Mat &	A,
		const PetscInt &	n,
		const PetscInt &	rowoffset = 0,
		const PetscInt &	coloffset = 0,
		const InsertMode &	addv = ADD_VALUES
	)

set a scaled matrix, (rows are scaled by matrix, using A=LA and MatDiagonalScale)

Returns

0 if successful

Parameters

[in]	diag_to_scale	premultple to scale the rows of Asub
[in]	Asub	sub matrix to set into mat
[in]	nsub	nxn size of square sub matrix Asub
[in,out]	A	Matrix A to set value (already initialized)
[in]	n	size of square Matrix A
[in]	rowoffset	start inserting Asub in A starting at rowoffset row
[in]	coloffset	start inserting Asub in A starting at coloffset column
[in]	addv	insert values or add values to matrix A

PetscInt SPE::set_P

(

SPE &

data

)

set permutation matrices and operators for use in OSS and SPE

Returns

0 if successful

Parameters

[in]

data

data class to have flags

PetscInt SPE::set_Vec	(	const PetscScalar *	bin,
		const PetscInt &	n,
		Vec &	b,
		const PetscBool &	parallel = PETSC_TRUE
	)

set a vector from PetscScalar 1D vector to PETSc Vec type in parallel

Returns

0 if successful

Parameters

[in]	bin	array set on all processors as 1D array
[in]	n	size of n array
[in,out]	b	Vec to SetValues and output in parallel (already initialized)
[in]	parallel	set in parallel

PetscInt SPE::set_Vec

(

Vec &

b

)

Assemble b vector.

Returns

0 if successful

Parameters

[in,out]

b

array to assemble on all processors

PetscInt SPE::set_Vec	(	const PetscScalar &	bin,
		const PetscInt &	n,
		Vec &	b
	)

set a vector from PetscScalar to PETSc Vec in location n

Returns

0 if successful

Parameters

[in]	bin	scalar to set into Vec
[in]	n	location to put into Vec
[in,out]	b	Vec to SetValues (already initialized)

PetscInt SPE::set_Vec	(	const Vec &	inVec,
		const PetscInt &	low,
		const PetscInt &	hi,
		Vec &	b
	)

set a subvector from larger vector from low to hi indices

Returns

0 if successful

Parameters

[in]	inVec	larger vec to copy values from
[in]	low	lower bound
[in]	hi	upper bound
[in,out]	b	Vec to SetValues and output (already initialized)

PetscInt SPE::set_Vec_linspace	(	PetscScalar	a,
		const PetscScalar	b,
		const PetscInt	n,
		PetscScalar	y[]
	)

set values of y, use linspace similar to matlab, creates on every processor

Returns

0 if successful

Parameters

[in]	a	lower bound
[in]	b	upper bound
[in]	n	upper bound
[out]	y	linspace output vector (already initialized to right size)

int SPE::trapz	(	const Vec &	q,
		PetscScalar &	I,
		SPE &	data
	)

trapezoidal rule on Vec with ny,nz values

Returns

0 if successful

Parameters

[in]	q	Vector to integrate
[out]	I	value of integration
[out]	data	data class to store Trapzy and Trapzz value and flags

PetscErrorCode SPE::trapz_4nynznt	(	const Vec &	q,
		PetscScalar &	I,
		SPE &	data
	)

trapezoidal rule on Vec with 4,ny,nz,nt values

Returns

0 if successful

Parameters

[in]	q	Vector to integrate
[out]	I	value of integration
[out]	data	data class to store Trapzy and Trapzz value and flags

int SPE::update_Closure	(	SPE &	data,
		Vec &	q,
		Vec &	qp1,
		PetscScalar &	alpha,
		const PetscInt &	maxiter = 50
	)

calculate the closure equation \( \int_\Omega \hat{\textbf{q}}^\dagger \hat{\textbf{q}}_x dy \) and output the result This is part of the solution procedure shown in the bottom half of this diagram

Solution Procedure

Returns

0 if successful

Parameters

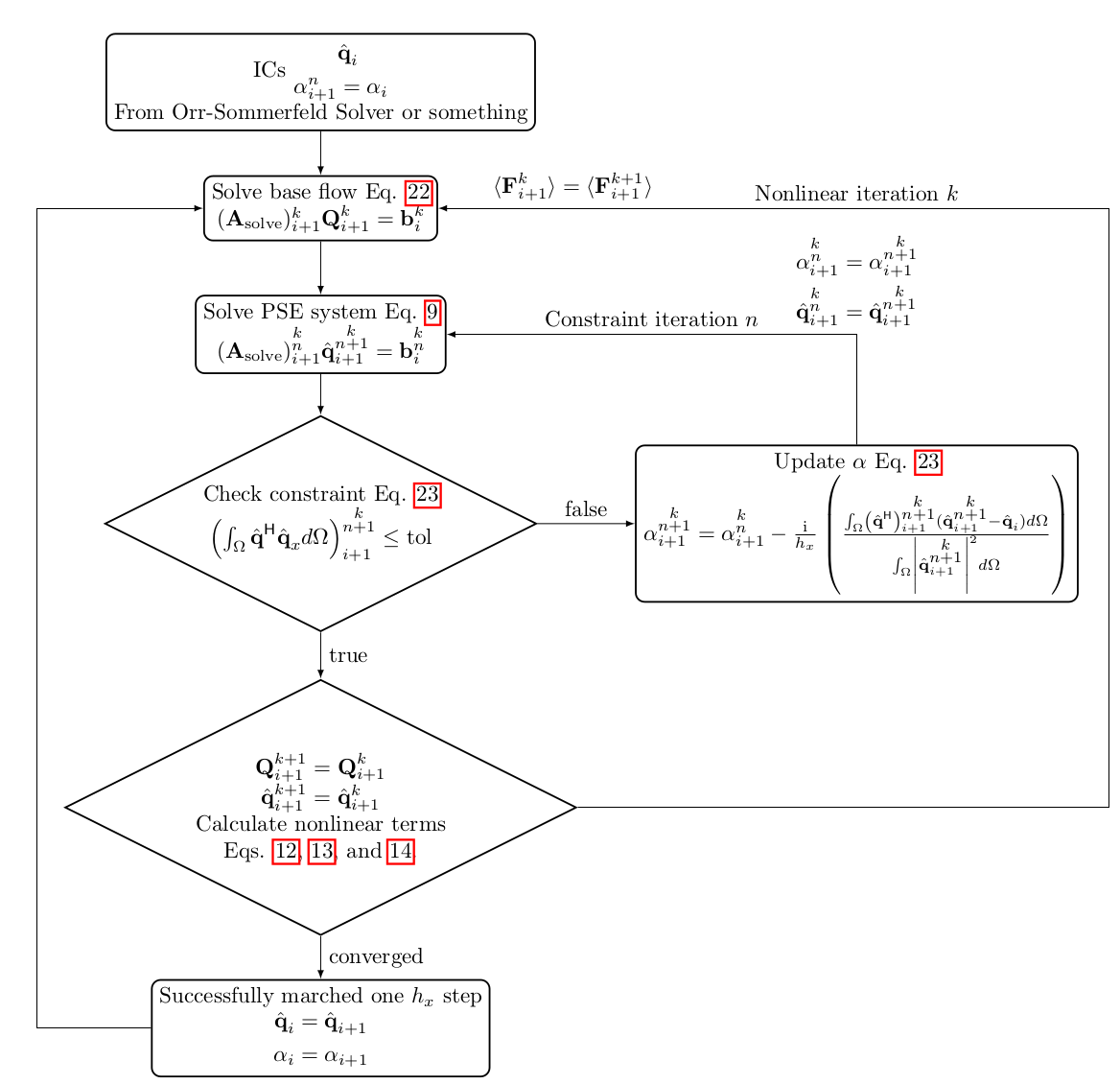
[in,out]	data	data class to store values
[in]	q	q at previous marching step
[in,out]	qp1	current marching step
[in,out]	alpha	\( \alpha \) value at current marching step
[in]	maxiter	maximum number of iterations (not implimented)

int SPE::update_Nonlinear	(	SPE &	data,
		Vec &	q,
		Vec &	qp1,
		PetscScalar &	alpha_old,
		PetscScalar &	alpha,
		PetscScalar &	Ialpha_old,
		PetscScalar &	Ialpha,
		const PetscInt &	maxiter = 50
	)

advance the Nonlinear SPE system one x step

Returns

0 if successful

Parameters

[in,out]	data	data class to store values
[in]	q	q at previous marching step
[in,out]	qp1	current marching step
[in,out]	alpha_old	\( \alpha \) value at previous marching step (will be updated)
[in,out]	alpha	\( \alpha \) value at current marching step
[in,out]	Ialpha_old	\( \int_{x_0}^{x_{i+1}} \alpha dx \) value at previous marching step
[in,out]	Ialpha	\( \int_{x_0}^{x_{i+1}} \alpha dx \) value at current marching step
[in]	maxiter	maximum number of iterations (not implimented)